lab03_Linear_Regression_and_How_to_minimize_cost

Original hypothesis

• Hypothesis : $H(x) = Wx + b$
• Cost : $cost(W,b) = \frac 1m \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)^2}$

Simplified hypothesis

• Hypothesis : $H(x) = Wx$
• Cost : $cost(W) = \frac 1m \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)^2}$

---

▷ What cost(W) looks like?

x	y
1	1
2	2
3	3

• W = 0, cost(W) = 4.67
  • $\frac 13((0 * 1 - 1)^2 + (0 * 2 - 2)^2 + (0 * 3 - 3)^2))$
• W = 1, cost(W) = 0
• W = 2, cost(W) = 4.67
• W = 3, cost(W) = 18.67

---

▷ Gradient descent algorithm

• Minimize cost function
• Gradient descent is used many minimization problems
• For a given cost function, cost(W,b), it will find W,b to minimize cost
• It can be applied to more general function: cost(w1, w2,...)

How it works?

• Strat with initial guesses
  • Start at 0,0 (or any other value)
  • Keeping changing W and b a little bit to try and reduce cost(W,b)
• Each time you change the parameters, you select the gradient which reduces cost(W,b) the most possible
• Repeat
• Do so until you converge to a local minimum
• Has an interesting property
  • Where you start can determine which minimum you end up

---

▷ Formal definition

$cost(W,b) = \frac 1m \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)^2}$

$cost(W,b) = \frac {1}{2m} \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)^2}$

---

$W := W - α\frac {∂}{∂W} \frac {1}{2m} \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)^2}$

$W := W - α\frac {∂}{∂W} \frac {1}{2m} \displaystyle\sum_{i=0}^{m}{2(Wx_i-y_i)x_i}$

$W := W - α\frac {∂}{∂W} \frac {1}{m} \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)x_i}$

• α : learning rate
• ∂ : partial differentiation for W

---

$W := W - α\frac {∂}{∂W}cost(W)$

1. differential cost and multiply it by α(learning rate)
2. subtract the calculated value from the existing W value
3. update the result value to W repeatedly #### (The larger learning rate, the more rapidly W changes)

---

▷ Convex function

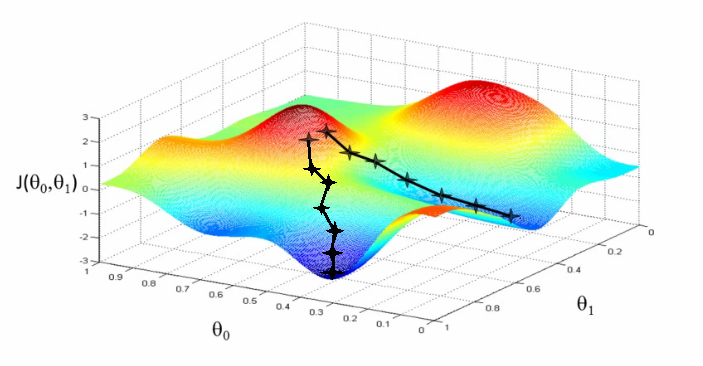
Local Minimum != Global Minimum ▶ we can't apply Gradient descent Algorithm

Local Minimum == Global Minimum ▶ we can apply Gradient descent Algorithm

We can be guaranteed the lowest point wherever you start

---

Simplified hypothesis

• Hypothesis : $H(x) = Wx$
• Cost : $cost(W) = \frac 1m \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)^2}$

▷ Cost function in pure Python

import numpy as np
X = np.array([1, 2, 3])
Y = np.array([1, 2, 3])

def cost_func(W, X, Y):
    c = 0
    for i in range(len(X)):
        c += (W * X[i] - Y[i]) ** 2
    return c / len(X)

for feed_W in np.linspace(-3, 5, num=15):
    curr_cost = cost_func(feed_W, X, Y)
    print("{:6.3f} | {:10.5f}".format(feed_W, curr_cost))

-3.000 |   74.66667
-2.429 |   54.85714
-1.857 |   38.09524
-1.286 |   24.38095
-0.714 |   13.71429
-0.143 |    6.09524
 0.429 |    1.52381
 1.000 |    0.00000
 1.571 |    1.52381
 2.143 |    6.09524
 2.714 |   13.71429
 3.286 |   24.38095
 3.857 |   38.09524
 4.429 |   54.85714
 5.000 |   74.66667

▷ Cost function in TensorFlow

import tensorflow as tf
X = np.array([1, 2, 3])
Y = np.array([1, 2, 3])

def cost_func(W, X, Y):
    hypothesis = X * W
    return tf.reduce_mean(tf.square(hypothesis - Y))

W_values = np.linspace(-3, 5, num=15)
cost_values = []

for feed_W in W_values:
    curr_cost = cost_func(feed_W, X, Y)
    cost_values.append(curr_cost)
    print("{:6.3f} | {:10.5f}".format(feed_W, curr_cost))

-3.000 |   74.66667
-2.429 |   54.85714
-1.857 |   38.09524
-1.286 |   24.38095
-0.714 |   13.71429
-0.143 |    6.09524
 0.429 |    1.52381
 1.000 |    0.00000
 1.571 |    1.52381
 2.143 |    6.09524
 2.714 |   13.71429
 3.286 |   24.38095
 3.857 |   38.09524
 4.429 |   54.85714
 5.000 |   74.66667

Gradient descent

• Cost : $cost(W) = \frac 1m \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)^2}$
• $W := W - α\frac {∂}{∂W} \frac {1}{m} \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)x_i}$

import tensorflow as tf
tf.random.set_seed(0)

X = [1., 2., 3., 4.]
Y = [1., 3., 5., 7.]

W = tf.Variable(tf.random.normal([1], -100., -100.)) # random value

for step in range(300):
    hypothesis = W * X
    cost = tf.reduce_mean(tf.square(hypothesis - Y))
    
    ## gradient descent code
    alpha = 0.01
    gradient = tf.reduce_mean(tf.multiply(tf.multiply(W, X) - Y, X))
    descent = W - tf.multiply(alpha, gradient)
    W.assign(descent)
    
    if step % 10 == 0:
        print('{:5} | {:10.4f} | {:10.6f}'.format(step, cost.numpy(), W.numpy()[0]))

    0 | 479206.3125 | -232.148300
   10 | 100776.1797 | -105.556763
   20 | 21193.1348 | -47.504101
   30 |  4457.0000 | -20.882177
   40 |   937.4286 |  -8.673835
   50 |   197.2708 |  -3.075305
   60 |    41.6172 |  -0.507918
   70 |     8.8836 |   0.669441
   80 |     1.9998 |   1.209356
   90 |     0.5522 |   1.456952
  100 |     0.2477 |   1.570495
  110 |     0.1837 |   1.622564
  120 |     0.1703 |   1.646442
  130 |     0.1674 |   1.657392
  140 |     0.1668 |   1.662413
  150 |     0.1667 |   1.664716
  160 |     0.1667 |   1.665772
  170 |     0.1667 |   1.666257
  180 |     0.1667 |   1.666479
  190 |     0.1667 |   1.666580
  200 |     0.1667 |   1.666627
  210 |     0.1667 |   1.666648
  220 |     0.1667 |   1.666658
  230 |     0.1667 |   1.666663
  240 |     0.1667 |   1.666665
  250 |     0.1667 |   1.666666
  260 |     0.1667 |   1.666666
  270 |     0.1667 |   1.666666
  280 |     0.1667 |   1.666666
  290 |     0.1667 |   1.666666