lab04_Multi_variable_linear_regression

▷ Recap

• Hypothesis : $H(x) = Wx + b$
• Cost function : $cost(W) = \frac 1m \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)^2}$
• gradient descent : $W := W - α\frac {∂}{∂W} \frac {1}{m} \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)x_i}$

---

▷ Hypothesis

• single variable
  • $H(x) = Wx + b$
• multi variable
  • $H(x_1,x_2,x_3) = w_1x_1 + w_2x_2 + w_3x_3 + b$

---

▷ Cost function

• single variable
  • $cost(W) = \frac 1m \displaystyle\sum_{i=0}^{m}{(Wx_i-y_i)^2}$
• multi variable
  • $H(x_1,x_2,x_3) = w_1x_1 + w_2x_2 + w_3x_3 + b$
  • $cost(W, b) = \frac 1m \displaystyle\sum_{i=0}^{m}{H(x_1,x_2,x_3)-y_i)^2}$

---

▷ Matrix multiplication

• $w_1x_1 + w_2x_2 + .. + w_nx_n$
  • It is cumbersome to have multi variables
  • So..

---

---

---

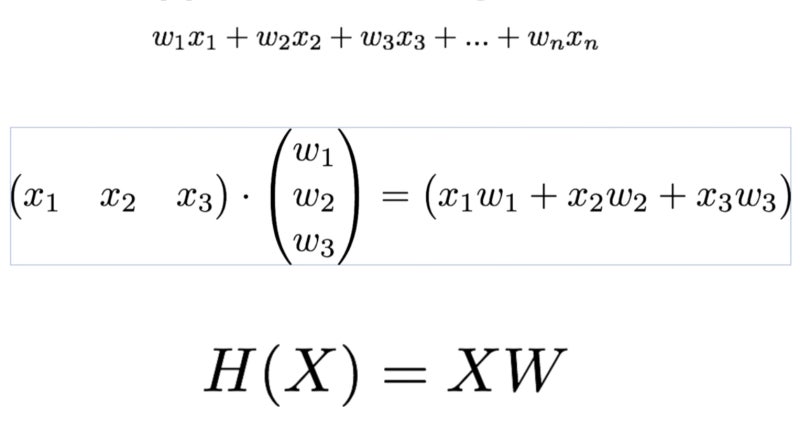
• $H(X) = XW$
• [5,3] * [3,1] = [5,1]
• [n,3] * [3,1] = [n,1]
  • We can ignore data numbers
• [n,3] * [x,y] = [n,2]
  • weight's row number(x) is equal to the input value's column number(3)
  • weight's column number(y) is equal to the output numbers(2)

---

▷ WX vs XW

• Lecture (theory)
  • $H(x) = Wx + b$
  • $h_𝜽(x) = 𝜽_1x + 𝜽_0$
  • $f(x) = ax + b$
• Implementation (TensorFlow)
  • $H(X) = XW$